【研究紹介】Redundancy test for some variables in linear discriminant analysis with two-step monotone incomplete data（2-step単調欠測データに基づく線形判別分析における一部の変数に対する冗長性検定）

更新日：2026年2月16日ページ番号：0008610

研究者プロフィール

岡田　悠希＜外部リンク＞（健康情報科学研究室　助教）
研究キーワード：漸近展開、バートレット修正、欠測データ、線形判別分析、最尤推定量、モンテカルロ・シミュレーション

研究紹介

研究テーマとその内容について教えてください。

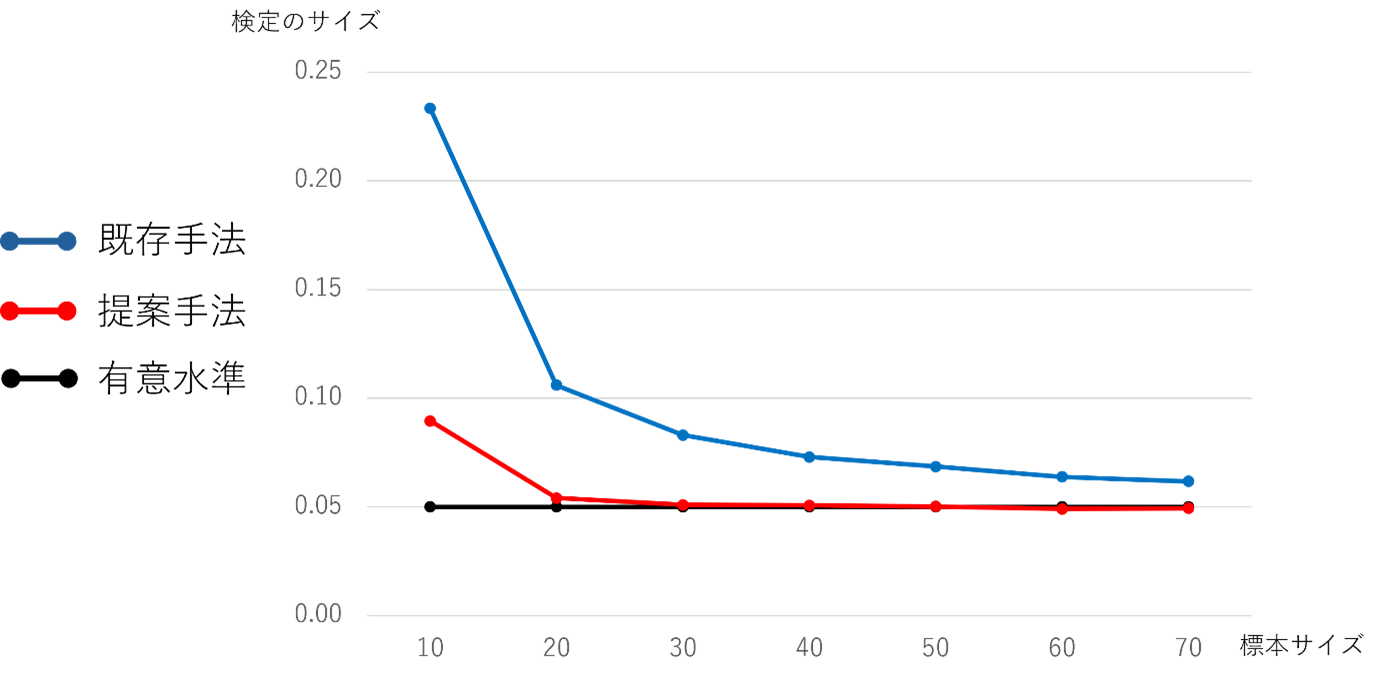
　本研究のテーマは、2-step単調欠測データを含む線形判別分析において、一部の変数が判別に寄与しない（冗長である）かどうかを評価する統計的検定法の開発です。具体的には、欠測を含む多変量正規分布データに基づいて尤度比検定統計量を導出し、さらにバートレット修正という手法を用いて、サンプルサイズが小さい場合でも第一種の過誤（誤って帰無仮説を棄却する確率）を適切に制御できる改良された検定手法を提案しました。シミュレーションの結果、提案手法は従来の尤度比検定よりも正確に有意水準を維持できることが示されました（図1）。

(図１)

シミュレーションの結果、提案手法は従来の尤度比検定よりも正確に有意水準を維持できることが示されました

現在の研究を始めようと思ったきっかけや、解決したい課題は何ですか？

　社会科学や医学、疫学、看護学などの研究分野では、回答拒否や無回答、パネル調査からの脱落等さまざまな理由により、データの一部が欠落した「不完全データ」に直面することが頻繁にあります。こうした状況下でも、コスト削減のために不要な変数を削減（変数選択）することは重要ですが、欠測データに基づく判別分析における変数選択の問題は、これまで十分な議論がなされていませんでした。そこで、欠測が存在する現実的なデータセットに対しても、統計的に信頼性の高い変数選択を可能にし、分析の精度と効率を両立させる手法を確立したいと考え、本研究に取り組みました。

先生の研究が、地域社会の中でどのように役立つと考えていますか？

　この研究は、特に医療現場や大規模な社会調査において実用的な価値があると考えています。例えば医療診断において、患者への身体的負担が大きい検査項目を含むデータがある場合、本手法を用いることで「診断精度を落とさずに省略可能な検査」を統計的根拠を持って特定できます。これにより、患者さんの負担軽減や医療コストの削減に貢献できます。また、アンケート調査等で未回答（欠測）が生じた場合でも、貴重なデータを破棄せず有効に活用し、正確な分析結果に基づいた政策提言や意思決定をサポートできると考えています。

この研究をどのように発展させていきたいですか？

　今後は、今回提案した検定手法の性能をより詳細に評価するため、尤度比検定の漸近的な検出力関数を導出することを目指しています。また、今回は特定の変数群全体に対する検定を行いましたが、より柔軟な変数選択が可能となるような形式への拡張も検討しています。さらに、検定手法だけでなく、AIC（赤池情報量規準）などのモデル選択規準におけるバイアス修正等にも本研究の知見を応用し、欠測データ解析における包括的な変数選択法を構築していきたいと考えています。